Originally posted on the discussion board of the Data Communications and Net-Centric Computing subject.

I am terrible at reading equations and much prefer explanations in human language. If your brain works like mine and had trouble wrapping your head around CRC, I hope my notes from this week’s tutorial help!

If you find it helpful please let me know, I may do another one on PAM which is on the assignment and people seem to have trouble with (at least in my class). If you already know this well, good on ya, I’m just trying to do a bit of rubberducking 🦆 to fortify my knowledge 🙂

Note

• Binary digits are also known as bits, I will be using them interchangeably 

What does the polynomial format mean? 

In this context, the polynomial is just another (more complex IMO) way of writing a binary number.

Let’s consider this week’s tutorial question, P(x)=x⁴+x+1. P(x) is basically the encoding scheme of a particular version of CRC. To me it is easier to understand in its binary form, and we can easily convert P(x) and the data between binary and polynomial:

• The n in xⁿ means the position of the digit, and n starts from 0. 
• If there is an xⁿ, e.g. x⁴, we then know that the 5th digit (remember, n starts at 0) will be 1.
• Similarly, x=x¹, meaning the 2nd digit will be 1.
• Since 1=x⁰ (basic maths), the first digit will also be 1. 
• Since x³ and x² do not exist in this polynomial, they will be 0. 

As a result, x⁴+x+1 can also be expressed as 10011 (binary).

The notes below visualises the process. It also explain how to convert a binary number to the polynomial format.

Calculating CRC using XOR method

Now that we know what the P(x) is in binary form, we can go to the next step and try to encode our data, 10010011011. My tutorial focused mainly on the method using the polynomial format, but I find using XOR easier and quicker. 

But first, if you don’t know what XOR is, it’s a logic that means eXclusive OR with the symbol ⊕. If you have taken electrical engineering classes you’ll definitely remember! 

XOR rules:

• If the two are different, the result is 1
• If the two are the same, the result is 0

XOR can also be done using binary subtraction.

• 1⊕1=0 (1-1=0)
• 0⊕0=0 (0-0=0)
• 1⊕0=1 (1-0=1)
• 0⊕1=1 (0-1=1 by pretending to borrow a bit, this may be tricky if you don’t know binary arithmetics)

Preparing the Data for XOR

Before finding out the CRC of the data, we need to pad it to compensate for the CRC that we will add later.

How many binary digits do we need to pad? Simply pull the n from the biggest xⁿ of the encoding scheme P(x). In our example, x⁴+x+1, we will need to pad the data by 4 bits.

Remembering that the data we’re trying to encode is 10010011011, we add four 0s to the end, making it 100100110110000, and this number is now ready for the next step!

To calculate the CRC checksum, line the data and the P(x) up as if you’re doing long division. Instead of dividing, you do binary subtraction or compare each binary digit (both valid) and write down the XOR result.

The CRC checksum is the remainder at the bottom, not the quotient at the top. You can see that I didn’t even bother to write down the quotient. Keep going until the remainder is smaller than the P(x) and you can’t do another one.

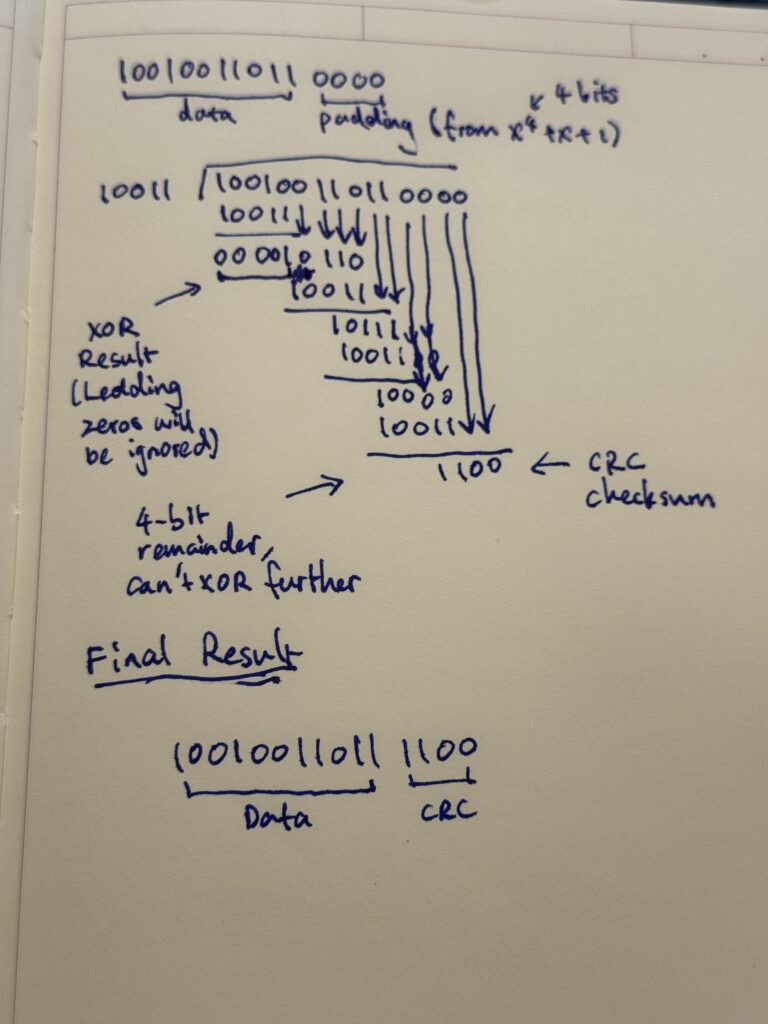
As a result, the CRC checksum is determined to be 1100 and the CRC-encoded data is 100100110111100.